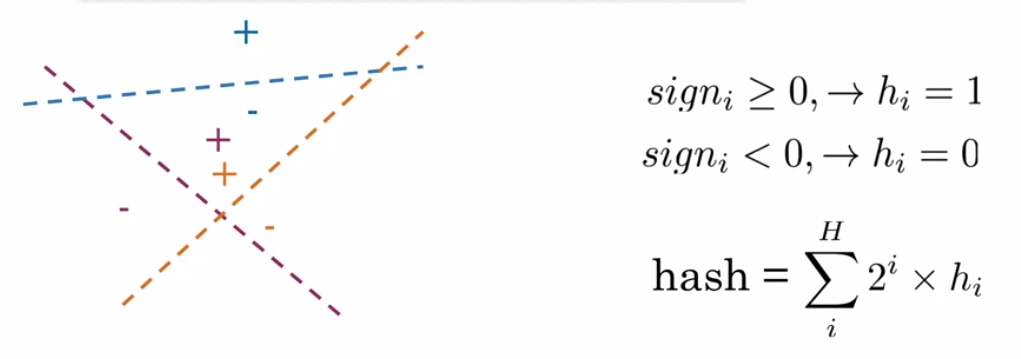Coursera NLP Module 1 Week 4 Notes
Machine Translation: An Overview
Transforming word vector
Given a set of english words X, a transformation matrix R and a desired set of french word Y the transformation
- \[XR \approx Y\]
- We initialize the weights R randomly and in a loop execute the following steps
- \[Loss = || XR - Y||_F\]
- \[g = \frac{d}{dR} Loss\]
- \[R = R - \alpha g\]
The Frobenius Norm takes all the squares of each elements of the matrix and sum them up.
- \[||A||_F = \sqrt{\sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2}\]
To simplify we can take the norm squared, thus:
- \[||A||^2_F = \sum_{i=1}^{m} \sum_{j=1}^{n} |a_{ij}|^2\]
Gradient:
- \[g = \frac{d}{dR} Loss = \frac{2}{m} (X^T (XR-Y))\]
Hash tables and hash functions
Hash might skip other proprieties of the itens being hashed.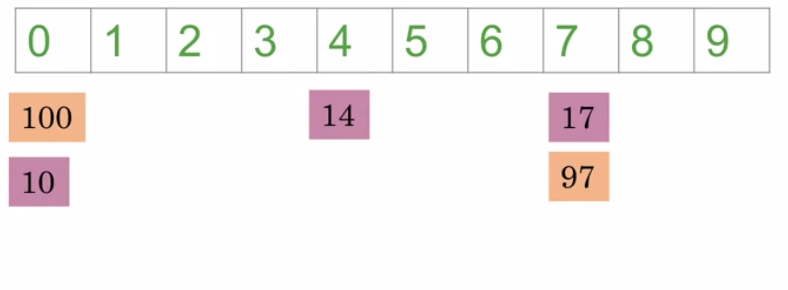 
To ensure that the itens are hashed accordingly we will use Locality sensitive hashing. 
Locality sensitive hashing
With multiple plans we can use a binary encoding to give the hash of the position given by the position. 