Coursera NLP Module 1 Week 3 Notes
Cosine Similarity
- Vector Norm \(||\overrightarrow{v}|| = \sqrt{\sum_{i=1}^n v_i^2}\)
-
Dot Product \(\overrightarrow{v} . \overrightarrow{w} = \sum_{i=1}^n v_i . w_i\)
- \[\overrightarrow{v} . \overrightarrow{w} = || \overrightarrow{v}|| \: ||\overrightarrow{w}|| cos(\beta)\]
- \[cos(\beta) = \frac{\overrightarrow{v} . \overrightarrow{w}}{|| \overrightarrow{v}|| \: ||\overrightarrow{w}||}\]
When $\beta$ is 90º the vector are maximal dissimilar, when it’s 0º the vectors are most similar and have cossine 1.
Manipulating Words in Vector Spaces
Given a trained vector space you can use a learnt representation to obtain new knowledge. Vectors of the words that occur in similar places in the sentence will be encoded in a similar way. You can take advantage of this type of consistency encoding to identify patterns.
Visualization and PCA
With PCA we can visualize higher dimension vector in 2 or 3 dimensions. PCA is an algorithm used for dimensionality reduction that can find uncorrelated features for your data. It’s very helpful for visualizing your data to check if your representation is capturing relationships among words.
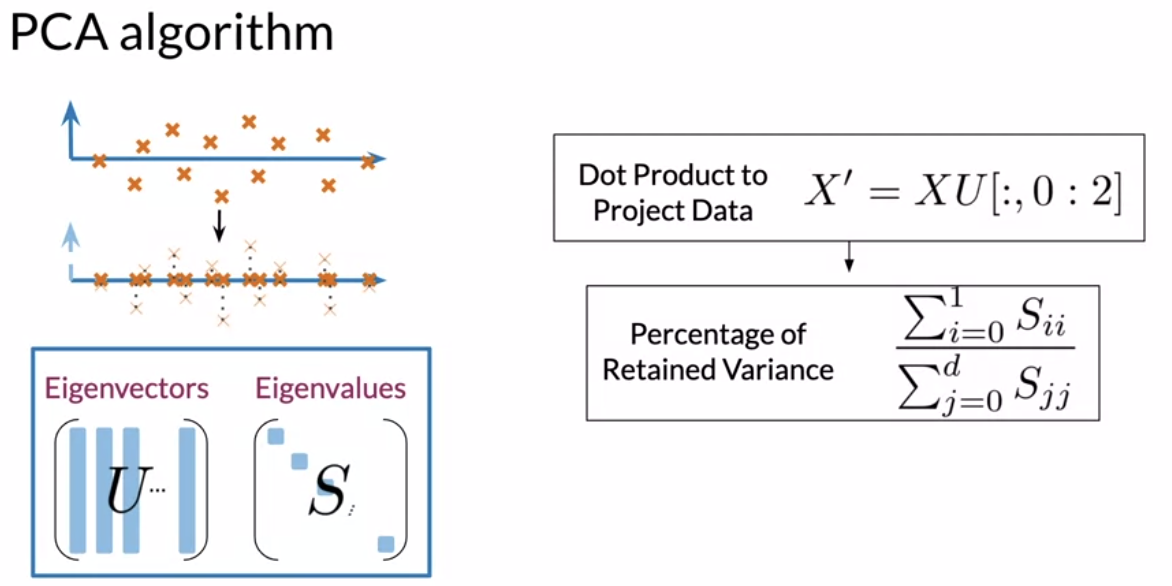
PCA Algorithm
- Eigenvector (Autovetor): Uncorrelated features for your data
- Eigenvalue (Autovalor): the amount of information retained by each feature