Coursera Deep Learning Module 5 Week 3 Notes

Basic Models
Sequence to Sequence Models
Machine Translation: Let a network encoder which encode a given sentence in one language be the input of a decoder network which outputs the sentence in a different language.
Paper: https://arxiv.org/pdf/1409.3215
Paper: https://arxiv.org/pdf/1406.1078
The same approach can be used for image captioning. The image can be convolved through a known convolution model and any intermediary representation can be used as input for the decoder to output a text sequence, the caption.
Paper: https://arxiv.org/pdf/1412.6632
Paper: https://arxiv.org/pdf/1411.4555
Paper: https://arxiv.org/pdf/1412.2306
Picking the most likely sentence
Greedy search might seems like a good option but actually it doesn’t usually help maximizing the output probability. If for each word we simply try to maximize $P(\hat{y}^{<1>} | x)$ for the first word and then $P(\hat{y}^{<1>}, \hat{y}^{<2>} | x)$ for the second word and so on we easily fall on some more common structures of the language that might not have been the best choice. To illustrate let’s take a model that is translating from the French “Jane visite l’Afrique en setembre” to English.
- “Jane is visiting Africa in September” looks like a good translation and is the most natural one
- “Jane is going to be visiting Africa in September” would be a possible output for greedy search because given that $P($Jane is going$| x) > P($Jane is visiting$ | x)$ simply because it’s more common to have sentences with the structure “is going”.
Beam Search
On each step where the greedy algorithm would only consider the highest probability of $P(\hat{y}^{<1>} | x)$ the Beam Search considers B options. For our example let’s take B as 3.
On the second step of the Beam Search for each one of the 3 first selected output words it would then calculate the highest probability of $P(\hat{y}^{<1>}, \hat{y}^{<2>} | x) = P(\hat{y}^{<1>}| x)P(\hat{y}^{<2>}| x, \hat{y}^{<1>})$, that means that the probability of the pair is conditioned to the probability of the first times the probability of the second given the first. In a scenario with 10k words as output we would have to evaluate B*10k = 30k, in our example. On the evaluation it’s only necessary to instantiate B separated networks to process each one of the previous maximized sequence. From all these pairs we again take the B pairs that maximize the probability and then keep repeating the algorithm.
Refinements to Beam Search
Given that the probabilities being multiplied are always numbers smaller than 1 we can easily fall into the problem of underflow. To avoid that we maximize the summation of log probabilities as we can see below. As the log is a strictly monotonic increasing function it’s guaranteed to converge together.
- $argmax \prod_{t=1}^{T_y} P(\hat{y}^{<t>} |x, \hat{y}^{<1>}, …, \hat{y}^{<t-1>})$
- $argmax \sum_{y=1}^{T_y} log P(\hat{y}^{<t>}|x, \hat{y}^{<1>}, …, \hat{y}^{<t-1>})$
As the multiplications over large sequences tend to go on the maximum probability tends to get smaller so the function tends to prefer shorter sentences unnaturally. To contour that we can add a normalizing factor as below:
$\frac{1}{T_y^{\alpha}} argmax \sum_{y=1}^{T_y} log P(\hat{y}^{<t>}|x, \hat{y}^{<1>}, …, \hat{y}^{<t-1>})$
Where $\alpha$ is a hyperparameter as $\alpha \in [0, 1]$ where on $\alpha = 0$ we would have no normalization and on $\alpha = 1$ we would have normalization by the lenght of the sentence. Setting $\alpha = 0.7$ allows for something in between.
How do you choose the width of your beam search? As B increases so does your computational processing. Large B guarantee better results but is much slower. Small B has worse results but works much faster. The B necessary depends on the application, the computational resources available and the amount of time available.
Unlike exact search algorithms like BFS (Breadth First Search) or DFS(Depth First Search), Beam Search runs faster but is not guaranteed to find exact maximum for $argmax P(y|x)$.
Error analysis in beam search
Given the expected response $y^{*}$ and the given output by the beam search algorithm $\hat{y}$ we would like to know how they correlate. We would like to inspect how $P(y^{*} | x)$ correlates to $P(\hat{y} | x)$. There are two possible options:
-
$P(y^{*} | x) > P(\hat{y} | x)$. What does this mean? It means that the Beam Search algorithm chose $\hat{y}$ even though $y^{*}$ attains higher $P(y^{*} | x)$. That means we should look into the Beam Search, probably increasing the width could have some benefits on allowing the algorithm to find $\hat{y}$.
-
$P(y^{*} | x) < P(\hat{y} | x)$. What does this mean? It means that the RNN model chose to give more relevance to the selected sequence, $\hat{y}$, even though $y^{*}$ is the desired output. That means we should look into the RNN model.
If any normalization is being used it should be the metric being evaluated instead of the Ps.
Given the scenario above it’s possible to carry on error analysis on the dev set which didn’t obtain the desired output and achieve an intuition of the problem source, either the Beam Search or the RNN model.
Bleu Score
One of the challenges of machine translation is that, given a French sentence, there could be multiple English translations that are equally good translations of that French sentence. So how do you evaluate a machine translation system if there are multiple equally good answers? The most commonly used approach is the BLEU score. BLEU stands for Bilingual Evaluation Understanding.
- French sentence: Le chat est sur le tapis
- Reference 1: The cat is on the mat
- Reference 2: There is a cat on the mat
- MT Output: the the the the the the the
- Precision: 7/7 (does the word appear in any reference? / total number of words)
- Modified Precision: 2/7 (max(sum(does the word appear in any reference?), total number of times the given word appears in the references) / total number of words)
This strategy also works on bigrams, trigrams or n-grams as desired using the same main idea. We can see the formalized idea below:
$ P_n = \frac{\sum_{ngrams \in \hat{y}} CountClip(ngrams)}{\sum_{ngrams \in \hat{y}} Count(ngrams)}$
The combined BLEU score is $BP * exp(\frac{1}{4} \sum_{n=1}^{4} P_n)$ where the BP stands for Brevity Penalty.
\[BP=\begin{cases} \displaystyle 1 \text{ if MT_output_length > reference_output_length } \\ \displaystyle exp(1 - \text{MT_output_length} / \text{reference_output_length}) \text{ otherwise} \end{cases}\]Paper: https://www.aclweb.org/anthology/P02-1040
Attention model intuition
Given a very long sentence, in a generic encoder-decoder model, we’re asking the model to encode all the sentence into the vector to than ask it to be completely unrolled on the decoder model. But it seem counterintuitive to think a human would do that: read a whole sentence in on language and then regurgitate it in the other language. Instead a human would translate it partially always going back to the input sentence as reference.
Given the RNN outputs on each time step an attention model is added on top of that to process a context vector. The context vector tries to answer: how much important is this information in the given step? And so it combines the intermediary context vectors and outputs the predicted word.
Paper: https://arxiv.org/pdf/1409.0473
Attention model
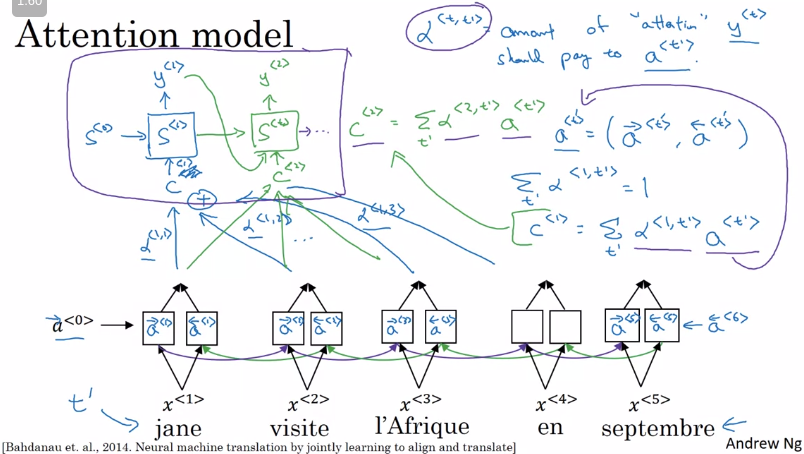
The sum of attentions in a given time step should be 1. Each $\alpha^{<t, t^{'}>}$ defines the amount of attention in the time step t that should be give to a given output activation $a^{<t^{'}>}$ generating the context vector $c^{<t>}$
$a^{<t^{'}>} = \frac{exp(e^{<t, t^{'}>})}{\sum_{t^{'} = 1}^{T_x} exp(^{<t, t^{'}>})}$
Visualizing the $a^{<t, t^{'}>$ matrix can give some insights of how the sequences are being aligned well. It’s pretty common to see in working models even language inversions that are not rpesent in one language but are in another.
Another situation that the the attention model can be beneficial is the date normalization problem whereas there are many different dates inputs and there’s an urge to normalize them to a single pattern.
Paper: https://arxiv.org/pdf/1502.03044
Speech Recognition
What is the speech recognition problem? You’re given an audio clip, x, and your job is to automatically find a text transcript, y. With end-to-end deep learning we’re able to realize that interpretable/hand-designed features as phonemes are not necessary.
CTC cost for speech recognition
Collapse repeated characters not separated by the ‘blank’ character
Paper: https://www.cs.toronto.edu/~graves/icml_2006.pdf
Trigger Word Detection
Given an audio clip input and a trigger word we would like that the output of the network was 0 if no trigger words was said and 1 if the trigger word was said. As this creates a very imbalanced dataset we can use a hack and insert 1s after the detected one to reduce the imbalance of the data.
Quiz
1.Consider using this encoder-decoder model for machine translation. This model is a “conditional language model” in the sense that the encoder portion (shown in green) is modeling the probability of the input sentence xx.
- True
- False
2.In beam search, if you increase the beam width BB, which of the following would you expect to be true? Check all that apply.
- Beam search will run more slowly.
- Beam search will use up more memory.
- Beam search will generally find better solutions (i.e. do a better job maximizing P(y∣x))
- Beam search will converge after fewer steps.
3.In machine translation, if we carry out beam search without using sentence normalization, the algorithm will tend to output overly short translations.
- True
- False
4.Suppose you are building a speech recognition system, which uses an RNN model to map from audio clip xx to a text transcript yy. Your algorithm uses beam search to try to find the value of yy that maximizes P(y∣x). On a dev set example, given an input audio clip, your algorithm outputs the transcript y^= “I’m building an A Eye system in Silly con Valley.”, whereas a human gives a much superior transcript y∗ = “I’m building an AI system in Silicon Valley.”
According to your model,
P(y^∣x)=1.09∗10−7 P(y∗∣x)=7.21∗10−8 Would you expect increasing the beam width B to help correct this example?
- No, because P(y∗∣x)≤P(y^∣x) indicates the error should be attributed to the RNN rather than to the search algorithm.
- No, because P(y∗∣x)≤P(y^∣x) indicates the error should be attributed to the search algorithm rather than to the RNN.
- Yes, because P(y∗∣x)≤P(y^∣x) indicates the error should be attributed to the RNN rather than to the search algorithm.
- Yes, because P(y∗∣x)≤P(y^∣x) indicates the error should be attributed to the search algorithm rather than to the RNN.
5.Continuing the example from Q4, suppose you work on your algorithm for a few more weeks, and now find that for the vast majority of examples on which your algorithm makes a mistake, P(y∗∣x)>P(y^∣x). This suggest you should focus your attention on improving the search algorithm.
- True
- False
6.Consider the attention model for machine translation.Further, here is the formula for $\alpha^{<t, t^{'}>}$. Which of the following statements about $\alpha^{<t, t^{'}>}$ are true? Check all that apply.
- We expect $\alpha^{<t, t^{'}>}$ to be generally larger for values of a<t′> that are highly relevant to the value the network should output for $y^{<t>}$. (Note the indices in the superscripts.)
- We expect $\alpha^{<t, t^{'}>}$ to be generally larger for values of $a^{<t>}$ that are highly relevant to the value the network should output for y<t′>. (Note the indices in the superscripts.)
- $\sum_t \alpha^{<t, t^{'}>}=1$ (Note the summation is over tt.)
- $\sum_{t^{'}} \alpha^{<t, t^{'}>}=1$ (Note the summation is over t'.)
7.The network learns where to “pay attention” by learning the values e<t,t′>, which are computed using a small neural network:
We can’t replace $s^{<t-1>}$ with $s^{<t>}$ as an input to this neural network. This is because s^{<t>} depends on $\alpha^{<t, t^{'}>}$ which in turn depends on $e^{<t, t^{'}>}$; so at the time we need to evaluate this network, we haven’t computed $s^{<t>}$ yet.
- True
- False
8.Compared to the encoder-decoder model shown in Question 1 of this quiz (which does not use an attention mechanism), we expect the attention model to have the greatest advantage when:
- The input sequence length T_x is large.
- The input sequence length T_x is small.
9.Under the CTC model, identical repeated characters not separated by the “blank” character (_) are collapsed. Under the CTC model, what does the following string collapse to?
__c_oo_o_kk___b_ooooo__oo__kkk
- cokbok
- cookbook
- cook book
- coookkboooooookkk
10.In trigger word detection, $x^{<t>}$ is:
- Features of the audio (such as spectrogram features) at time t.
- The t-th input word, represented as either a one-hot vector or a word embedding.
- Whether the trigger word is being said at time t.
- Whether someone has just finished saying the trigger word at time t.