Coursera Deep Learning Module 5 Week 1 Notes

Why sequential models

Work best with sequential data as:

• Speech Recognition
• Music Generation
• Sentiment Classification
• DNA Sequence Analysis
• Machine Translation
• Video Activity Recognition
• Name Entity Recognition

The given inputs may or may not be of the same kind or even have the same length.

Notation

Given an input x we would have $x^{<i>}$ as the ith word in the sentence, for example. $T_x$ denote how long the sequence is. In named entity recognition we could have the same length in the output denoted by $T_y$ where each $y^{<i>}$ denotes a given output.

A common way to vectorize the given input $x^{<i>}$ is using one hot encoded vectors. In this encoding each position of the vector represent a word.

Recurrent Neural Network Model

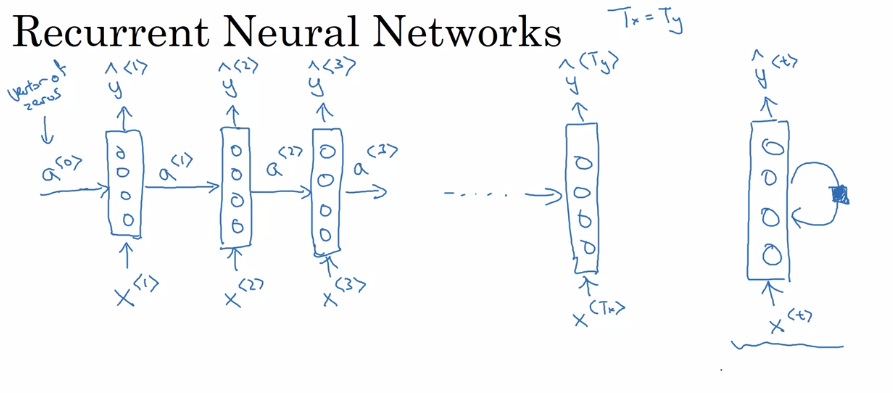
A limitation of this type of network is that only uses information from the past of the sequences.

• $a^{<0>} = \overrightarrow{0}$
• $a^{<t>} = g_1(W_{aa} a^{<t-1>} + W_{ax} x^{<t>} + b_a)$

• $\hat{y}^{<t>} = g_2(W_{ya} a^{<t>} + b_y)$

• $a^{<t>} = g_1(W_{a} [a^{<t-1>} ,x^{<t>}] + b_a)$
• $[W_{aa} W_{ax}] = W_a$

Backpropagation through time

The loss for each time step prediction can be given as $\mathcal{L}(\hat{y}^{<t>}, y^{<t>}) = - y^{<t>}\log\hat{y}^{<t>} - (1-y^{<t>})\log(1-\hat{y}^{<t>})$ and the overall loss is simply the sum of each time step as $\mathcal{L}(\hat{y}, y) = \sum_{t=1}^{T_y} \mathcal{L}(\hat{y}^{<t>}, y^{<t>})$.

Different types of RNNs

$T_x$ and $T_y$ might not always be the same.

Reference: http://karpathy.github.io/2015/05/21/rnn-effectiveness/

Language model and sequence generation

A language modelling gives a probability of a given sentence of happening in a real context.

The first step given an input is to tokenize it and then vectorize it. A language model has a softmax output size as the number of tokens it’s using. If the output is the number of words it’s not uncommon to have outputs on the hundreds or thousands of outputs. In a sequence training the outputs are already well defined but in the inference time the sequences can be generated.

Sampling novel sequences

Given a softmax output with thousands of words we can, instead of taking always the highest value in the output, take some value around it given some variation. Using this sampling instead of always selecting the highest output prediction allows the sequence generated to be much more unconstrained and flexible in its generation.

Depending on the application instead of using words using character-level language model might be more interesting. The pro is that you never have unknown words and the dimensions are usually much smaller to deal than the word level. This models are much more robust to noise than its counterpart word.

Vanishing gradients with RNNs

In long sequences we have the same problem as very deep neural networks where the gradient can either explode or vanish. The exploding gradients problem is rather rare and possibly easier to address as we could simply clip it to stop it from growing. The vanishing on other hand can be partially solved with good parameter initialization but will keep happening in long structures. To address this problem other units have been developed.

Gated Recurrent Unit (GRU)

• ${\tilde{c}}^{<t>} = tanh(W_c [ \Gamma_r * c^{<t-1>}, x^{<t>} ] + b_c) $
• $\Gamma_u = \sigma (W_u [c^{<t-1>}, x^{<t>}] + b_u)$
• $\Gamma_r = \sigma (W_r [c^{<t-1>}, x^{<t>}] + b_r)$
• $c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + (1-\Gamma_u) * c^{<t-1>} $

Long Short Term Memory (LSTM)

• ${\tilde{c}}^{<t>} = tanh(W_c [ a^{<t-1>}, x^{<t>} ] + b_c) $
• $\Gamma_u = \sigma (W_u [a^{<t-1>}, x^{<t>}] + b_u)$
• $\Gamma_f = \sigma (W_f [a^{<t-1>}, x^{<t>}] + b_f)$
• $\Gamma_o = \sigma (W_o [c^{<t-1>}, x^{<t>}] + b_o)$
• $c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + \Gamma_f * c^{<t-1>} $
• $a^{<t>} = \Gamma_o * tanh c^{<t>} $

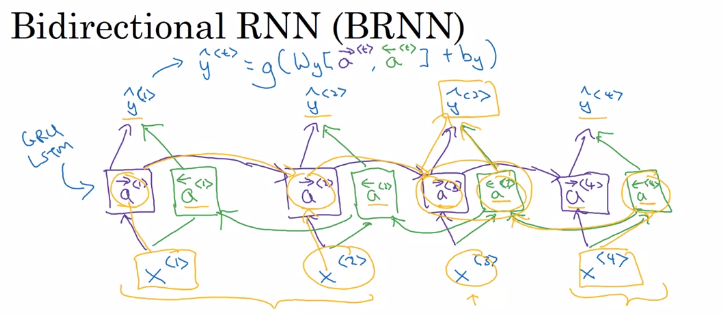
Bidirectional RNN

Bidirectional RNNs lets you take information from both earlier and later in the sequence. An output for a given time step is due the forward pass and the backward pass combined as we can see in the equation

• $\hat{y}^{<t>} = g(W_y[\overrightarrow{a}^{<t>}, \overleftarrow{a}^{<t>}] + b_y)$

Deep RNNs

It’s basically stacked recurrent units. A standard RNN could output on each step the output by itself but stacking the units make the intermediary units wait for the initial inputs to compute its activations. As the temporal dimension already adds lots of dimensions it’s not common to see many units stacked together. One thing that it’s commonly used is a plain neural network in the output of the recurrent part.

Quiz

1.Suppose your training examples are sentences (sequences of words). Which of the following refers to the j^{th} word in the i^{th} training example?

• $x^{(i)<j>}$
• $x^{<i>(j)}$
• $x^{(j)<i>}$
• $x^{<j>(i)}$

2.Consider this RNN. This specific type of architecture is appropriate when:

• $T_x = T_y$
• $T_x < T_y$
• $T_x > T_y$
• $T_x = 1$

3.To which of these tasks would you apply a many-to-one RNN architecture? (Check all that apply).

• Speech recognition (input an audio clip and output a transcript)
• Sentiment classification (input a piece of text and output a 0/1 to denote positive or negative sentiment)
• Image classification (input an image and output a label)
• Gender recognition from speech (input an audio clip and output a label indicating the speaker’s gender)

4.You are training this RNN language model. At the t^{th} time step, what is the RNN doing? Choose the best answer.

• Estimating $P(y^{<1>},y^{<2>},…,y^{<t−1>})$
• Estimating $P(y^{<t>})$
• Estimating $P(y^{<t>}∣y^{<1>},y^{<2>},…,y^{<t−1>})$
• Estimating $P(y^{<t>}∣y^{<1>},y^{<2>},…,y^{<t>})$

5.You have finished training a language model RNN and are using it to sample random sentences, as follows:

What are you doing at each time step tt?

• (i) Use the probabilities output by the RNN to pick the highest probability word for that time-step as $y^{<t>}$. (ii) Then pass the ground-truth word from the training set to the next time-step.
• (i) Use the probabilities output by the RNN to randomly sample a chosen word for that time-step as $y^{<t>}$. (ii) Then pass the ground-truth word from the training set to the next time-step.
• (i) Use the probabilities output by the RNN to pick the highest probability word for that time-step as $y^{<t>}$. (ii) Then pass this selected word to the next time-step.
• (i) Use the probabilities output by the RNN to randomly sample a chosen word for that time-step as $y^{<t>}$. (ii) Then pass this selected word to the next time-step.

6.You are training an RNN, and find that your weights and activations are all taking on the value of NaN (“Not a Number”). Which of these is the most likely cause of this problem?

• Vanishing gradient problem.
• Exploding gradient problem.
• ReLU activation function g(.) used to compute g(z), where z is too large.
• Sigmoid activation function g(.) used to compute g(z), where z is too large.

7.Suppose you are training a LSTM. You have a 10000 word vocabulary, and are using an LSTM with 100-dimensional activations $a^{<t>}$. What is the dimension of $\Gamma_u$ at each time step?

• 1
• 100
• 300
• 10000

8.Here’re the update equations for the GRU. Alice proposes to simplify the GRU by always removing the $\Gamma_u$. I.e., setting $\Gamma_u$ = 1. Betty proposes to simplify the GRU by removing the $\Gamma_r$. I. e., setting $\Gamma_r$ = 1 always. Which of these models is more likely to work without vanishing gradient problems even when trained on very long input sequences?

• Alice’s model (removing $\Gamma_u$), because if $\Gamma_r \approx 0$ for a timestep, the gradient can propagate back through that timestep without much decay.
• Alice’s model (removing $\Gamma_u$), because if $\Gamma_r \approx 1$ for a timestep, the gradient can propagate back through that timestep without much decay.
• Betty’s model (removing $\Gamma_r$), because if $\Gamma_u \approx 0$ for a timestep, the gradient can propagate back through that timestep without much decay.
• Betty’s model (removing $\Gamma_r$), because if $\Gamma_u \approx 1$ for a timestep, the gradient can propagate back through that timestep without much decay.

9.Here are the equations for the GRU and the LSTM. From these, we can see that the Update Gate and Forget Gate in the LSTM play a role similar to ___ and __ in the GRU. What should go in the the blanks?

• $\Gamma_u$ and 1−$\Gamma_u$
• $\Gamma_u$ and $Gamma_r$
• 1−$\Gamma_u$ and $\Gamma_u$
• $Gamma_r$ and $\Gamma_u$

10.You have a pet dog whose mood is heavily dependent on the current and past few days’ weather. You’ve collected data for the past 365 days on the weather, which you represent as a sequence as x<1>,…,x<365>. You’ve also collected data on your dog’s mood, which you represent as y<1>,…,y<365>. You’d like to build a model to map from x \rightarrow yx→y. Should you use a Unidirectional RNN or Bidirectional RNN for this problem?

• Bidirectional RNN, because this allows the prediction of mood on day t to take into account more information.
• Bidirectional RNN, because this allows backpropagation to compute more accurate gradients.
• Unidirectional RNN, because the value of $y^{<t>}$ depends only on $x^{<1>},…,x^{<t>}$, but not on $x^{<t+1>},…,x^{<365>}$
• Unidirectional RNN, because the value of $y^{<t>}$ depends only on $x^{<t>}$, and not other days’ weather.