Coursera Deep Learning Module 4 Week 2 Notes

Why look at case studies?
In summary, to gain intuition how to build convnets. Classic networks discussed: LeNet5, AlexNet, VGG. Other networks: ResNet and Inception.
Classic Networks
LeNet-5
Input: $32 \times 32 \times 1$ (only 1 channel because the images are grey-scale) Classify handwritten digits into one of 10 available categories. It has about 60k parameters, $n_H, n_W$ decreases as the network deepens
Paper: http://yann.lecun.com/exdb/publis/pdf/lecun-98.pdf
AlexNet
Input: $227 \times 227 \times 3$ (RGB images) Classify 1000 image classes on the ImageNet competition. It has about 60M parameters
VGG-16
Input: $224 \times 224 \times 3$ (RGB images) All the layers are alternating between CONV with $3 \times 3$ filters and MAX-POOL with $2 \times 2$ filter and $s=2$. Its name has 16 because that’s how many conv layers it has. It has 160M parameters
Paper: https://arxiv.org/pdf/1409.1556.pdf
ResNets
Very, very deep neural networks are difficult to train because of vanishing and exploding gradient types of problems. Skip connections allows you to take the activation from one layer and feed it to another layer even much deeper in the neural network. Using that technique that ResNet was built upon enabling it to train very, very deep networks.
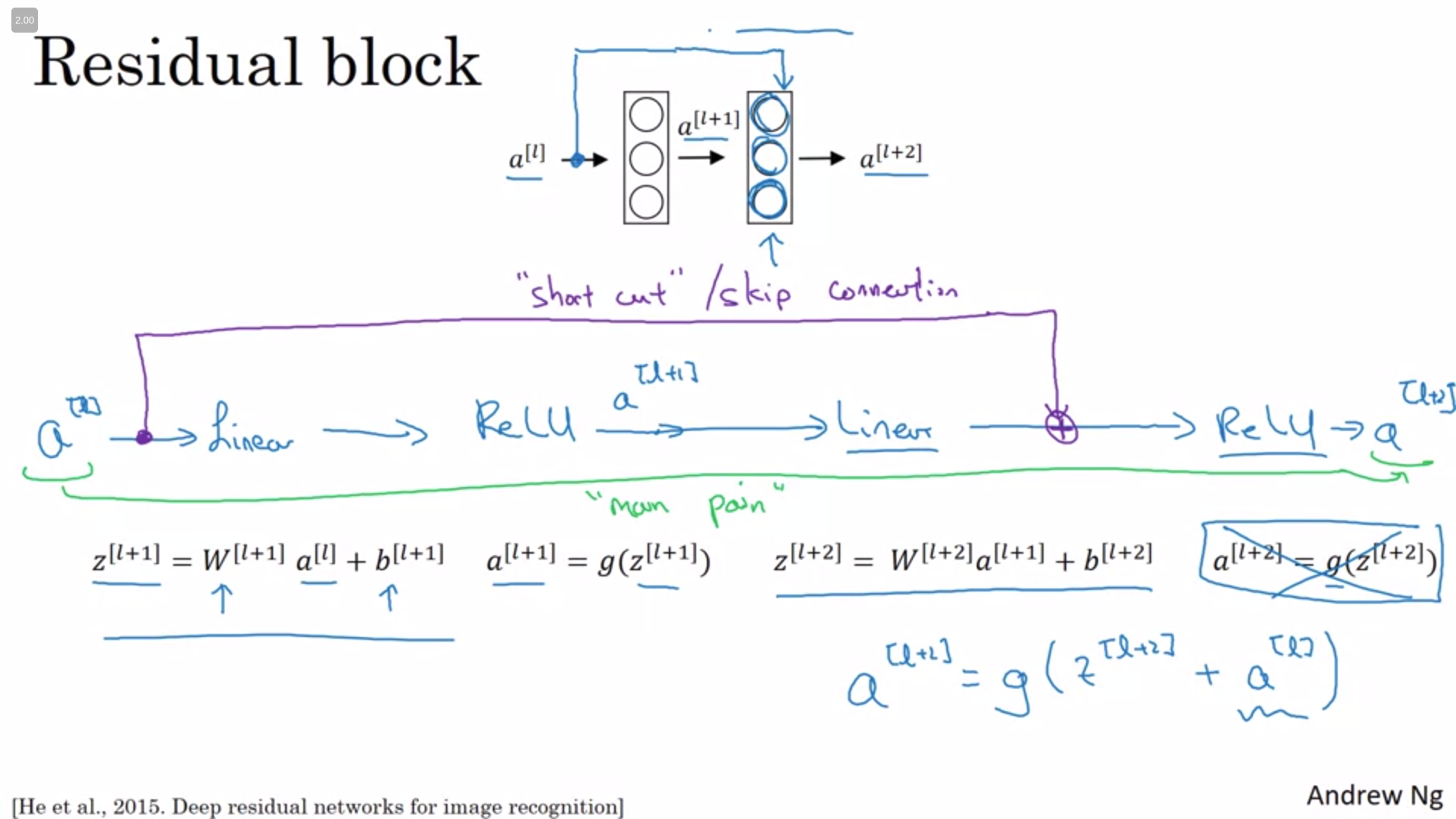
Why ResNets Work
As we can see below is easier for the network to learn the identity function which means that the network can decide to take into account a transformed value or the input value (or a combination of both) to perform its computation.
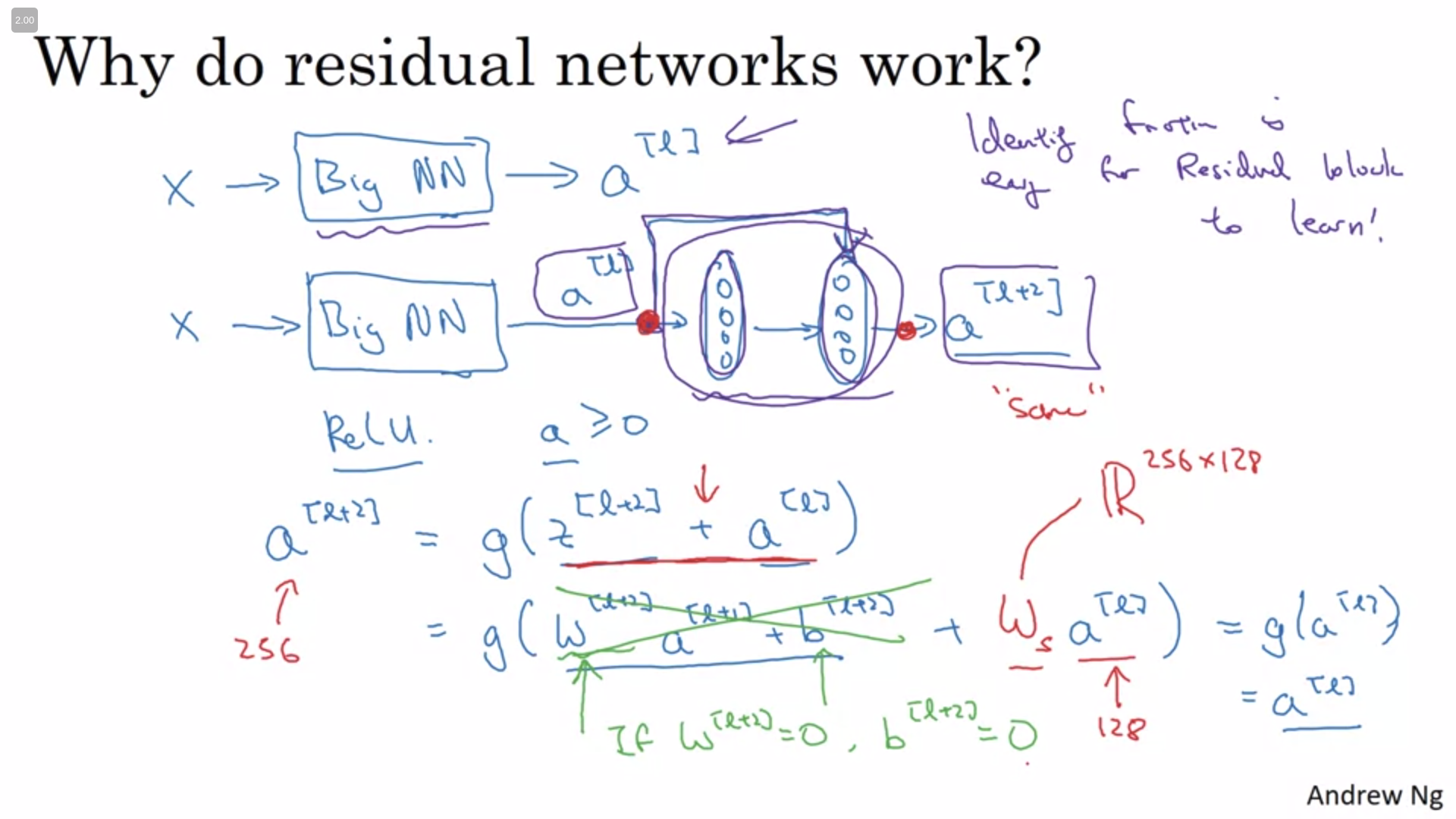
The skip connection assume that the dimensions will be the same. But as pointed above even if the dimensions are not the same an intermediary matrix $w_s$ can be added to the equation to ensure that the dimensions match. This matrix can be fixed or learnable and either work.
Paper: https://arxiv.org/pdf/1512.03385.pdf
Networks in Networks and 1x1 Convolutions
If you have a $6 \times 6 \times 32$ input a convolution with a $1 \times 1$ will look at each of the 32 different channels in that position, take the element wise product between them and then apply a ReLU non-linearity.
One way to think about this operation is as each one of the channels (32 in the example above) are being feeded into a neuron which is multiplying them by 32 weights and applying a ReLU non-linearity. If you have no one filter but many $1 \times 1$ filters your output will have the $n_c$ correspondent which each one can be thought as a network in network. This operation can carry pretty complex computations in your network without being explicitly too hard.
If you wanted to shrink the height and width you could use a pooling layer but to shrink the number of channels you can use a $1 \times 1$ convolution.
Paper: https://arxiv.org/pdf/1312.4400.pdf
Inception Network Motivation
Instead of choosing a kernel size use them all. To ensure that the outputs of the different kernels match up use a same padding. MaxPooling can also be used but in this situation it’s necessary to use padding to match up the sizes. One of the main problems here is computational cost with this approach.
Inspecting only the $5 \times 5$ convolution with 32 filters and a $28 \times 28 \times 192$ input we can assess that the total number of multiplications is about $ 28 * 28 * 32 * 5 * 5 * 192 = 120M$.
It’s possible to cut the cost to a tenth of that using $1 \times 1$ convolution using it as a first step in the computation. Given the same input we could compute the $1 \times 1$ convolution with 16 filters computing $28 * 28 * 16 * 1 * 1 * 16 = 2.4M$ computations. If we carry to the proper $5 \times 5$ filter with 32 filters we would carry $28 * 28 * 32 * 5 * 5 * 16 = 10M$. Summing up you have about $12.4M$ which is about a tenth of the previous scenario.
You might be wondering: Does shrinking down the representation size so dramatically hurts the performance of your neural network? As long as you implement this bottleneck layer within reason, you can shrink down the representation size significantly and it doesn’t seem to hurt the performance, but saves you a lot of computation.
Paper: https://arxiv.org/pdf/1409.4842.pdf
Inception Network
Each module has 4 parallel computations:
- $1 \times 1$
- $1 \times 1$ -> $3 \times 3$
- $1 \times 1$ -> $5 \times 5$
- MAXPOOL with Same Padding -> $1 \times 1$
The 4th (MaxPool) could add lots of channels in the output and the $1 \times 1$ conv is added to reduce the amount of channels. One particularity of the GoogLeNet is that it has some softmax branches in the middle of the inception modules to ensure that even the intermediary blocks can classify the images particularly well.
Using Open-Source Implementation
A lot of these neural networks are difficult or finicky to replicate because a lot of details about tuning of the hyperparameters, such as learning decay, make some difference to the performance. It’s common to see even high specialized people manifesting difficulties to replicate someone else’s polished work just from reading their paper. Fortunately, a lot of deep learning researchers routinely open source their work on the Internet, such as on GitHub, easening the replication process. If you can get the author’s implementation, you can usually get going much faster than if you would try to reimplement it from scratch. Although sometimes reimplementing from scratch could be a good exercise to do as well.
Transfer Learning
Rather than training the ways from scratch, from random initialization, you often make much faster progress if use someone else’s trained network architecture to use that as pre-training and transfer that to a new task that you might be interested in. The community has been pretty active either on making datasets available(Image Net, MS COCO, Pascal) and sharing pre-trained models.
Sometimes these training takes several weeks and might take many GPUs and the fact that someone else has done this and gone through the painful high-performance search process, means that you can often download open source ways that took someone else many weeks or months to figure out and use that as a very good initialization for your own neural network. And use transfer learning to sort of transfer knowledge from some of these very large public data sets to your own problem.
Data Augmentation
Data augmentation is one of the techniques that is often used to improve the performance of computer vision systems. Perhaps the simplest data augmentation method is mirroring on the vertical axis. Another commonly used technique is random cropping. It isn’t a perfect data augmentation technique as you could randomly end up taking a crop which doesn’t look like the class you’re trying to predict. In practice works reasonably well as long as your random crops are reasonably large subsets of the actual image.
The second type of data augmentation that is commonly used is color shifting: given a picture you add distortions to the R, G and B channels. The motivation for this technique is to provide correction for any color aberration present and also make the algorithm mainly robust to color variations as the objects being classified don’t change.
There are different ways to sample R, G, and B. One of the ways to implement color distortion uses an algorithm called PCA, sometimes called PCA Color Augmentation. The rough idea is that it keeps the overall color of the tint the same while still sampling around.
Data augmentation process also has a few hyperparameters such as how much color shifting do you implement and exactly what parameters you use for random cropping. Similar previous advices, a good place start might be using someone else’s implementation or parameters. Naturally that if you have some specific objective in mind it might be reasonable also to determine hyperparameters yourself.
State of Computer Vision
You can think of most machine learning problems as falling somewhere on the spectrum between where you have relatively little data to where you have lots of data. You see that, on average, when there’s lot of data available it’s more common to find people presenting simpler algorithms as well as less hand-engineering features. There’s less need to carefully design features for the problem because you can have a giant neural network to figure it out for you. Whereas, in contrast, when you don’t have that much data then, on average, you see people engaging in more hand-engineering and more “hacks”. But when you don’t have much data then hand-engineering is actually the best way to get good performance.
Machine learning algorithms usually have two sources of knowledge:
- Labeled data
- Hand-engineering
There are lots of ways to hand-engineer a system:
- hand designing the features
- hand designing the network architectures
- hand designing other components of your system, etc
When you don’t have much labeled data you just have to call more on hand-engineering. Historically this is what happened to get where we are right now.
Quiz
1.Which of the following do you typically see as you move to deeper layers in a ConvNet?
- nH and nW increases, while nC decreases
- nH and nW decreases, while nC also decreases
- nH and nW increases, while nC also increases
- nH and nW decrease, while nC increases
2.Which of the following do you typically see in a ConvNet? (Check all that apply.)
- Multiple CONV layers followed by a POOL layer
- Multiple POOL layers followed by a CONV layer
- FC layers in the last few layers
- FC layers in the first few layers
3.In order to be able to build very deep networks, we usually only use pooling layers to downsize the height/width of the activation volumes while convolutions are used with “valid” padding. Otherwise, we would downsize the input of the model too quickly.
- True
- False
4.Training a deeper network (for example, adding additional layers to the network) allows the network to fit more complex functions and thus almost always results in lower training error. For this question, assume we’re referring to “plain” networks.
- True
- False
5.The following equation captures the computation in a ResNet block. What goes into the two blanks above? a[l+2]=g(W[l+2]g(W[l+1]a[l]+b[l+1])+bl+2+___ )+___
- a[l] and 0, respectively
- 0 and z[l+1], respectively
- z[l] and a[l], respectively
- 0 and a[l], respectively
6.Which ones of the following statements on Residual Networks are true? (Check all that apply.)
- The skip-connection makes it easy for the network to learn an identity mapping between the input and the output within the ResNet block.
- Using a skip-connection helps the gradient to backpropagate and thus helps you to train deeper networks
- A ResNet with L layers would have on the order of $L^2$ skip connections in total.
- The skip-connections compute a complex non-linear function of the input to pass to a deeper layer in the network.
7.Suppose you have an input volume of dimension 64x64x16. How many parameters would a single 1x1 convolutional filter have (including the bias)?
- 17
- 1
- 4097
- 2
8.Suppose you have an input volume of dimension nH x nW x nC. Which of the following statements you agree with? (Assume that “1x1 convolutional layer” below always uses a stride of 1 and no padding.)
- You can use a 1x1 convolutional layer to reduce nC but not nH, nW.
- You can use a 1x1 convolutional layer to reduce nH, nW, and nC.
- You can use a pooling layer to reduce nH, nW, but not nC.
- You can use a pooling layer to reduce nH, nW, and nC.
9.Which ones of the following statements on Inception Networks are true? (Check all that apply.)
- Inception networks incorporates a variety of network architectures (similar to dropout, which randomly chooses a network architecture on each step) and thus has a similar regularizing effect as dropout.
- Making an inception network deeper (by stacking more inception blocks together) should not hurt training set performance.
- Inception blocks usually use 1x1 convolutions to reduce the input data volume’s size before applying 3x3 and 5x5 convolutions.
- A single inception block allows the network to use a combination of 1x1, 3x3, 5x5 convolutions and pooling.
10.Which of the following are common reasons for using open-source implementations of ConvNets (both the model and/or weights)? Check all that apply.
- The same techniques for winning computer vision competitions, such as using multiple crops at test time, are widely used in practical deployments (or production system deployments) of ConvNets.
- Parameters trained for one computer vision task are often useful as pretraining for other computer vision tasks.
- A model trained for one computer vision task can usually be used to perform data augmentation even for a different computer vision task.
- It is a convenient way to get working an implementation of a complex ConvNet architecture.