Coursera Deep Learning Module 2 Week 1 Notes

Train/Dev/Test Sets
- Applied ML is a highly iterative process
- Start with an idea, implement it in a code and experiment
- Previous era: 70/30 or 60/20/20
- Modern big data era: 98/1/1 or 99.5/0.25/0.25
- The dev set is simply a way to compare the real performance across algorithms
- The test set is to guarantee the real generalization of the model
- Mismatched train/test distribution
- Training set: Cat pictures from webpages
- Dev/test set: Cat pictures from users using your app
- Different resolutions, different image (data) quality
- Make sure that dev and test set have the same distribution as your train set
- It might be okay not to have a test set but the evaluation must be made to a different data set which hasn’t been seen by the model, like production
Bias/Variance
- Underfitting x Overfitting
- Train set error: 1% x Dev set error: 11% -> High variance
- Train set error: 15% x Dev set error: 16%. Assuming that humans obtain error ~0% -> High Bias because the algorithm isn’t even fitting the training set well
- Train set error: 15% x Dev set error: 30% -> High Bias and high variance
- Train set error: 0.5% x Dev set error: 1% -> Low bias and low variance
- All these assumptions are based on the assumption that the human error, or optimal base error is close to 0%
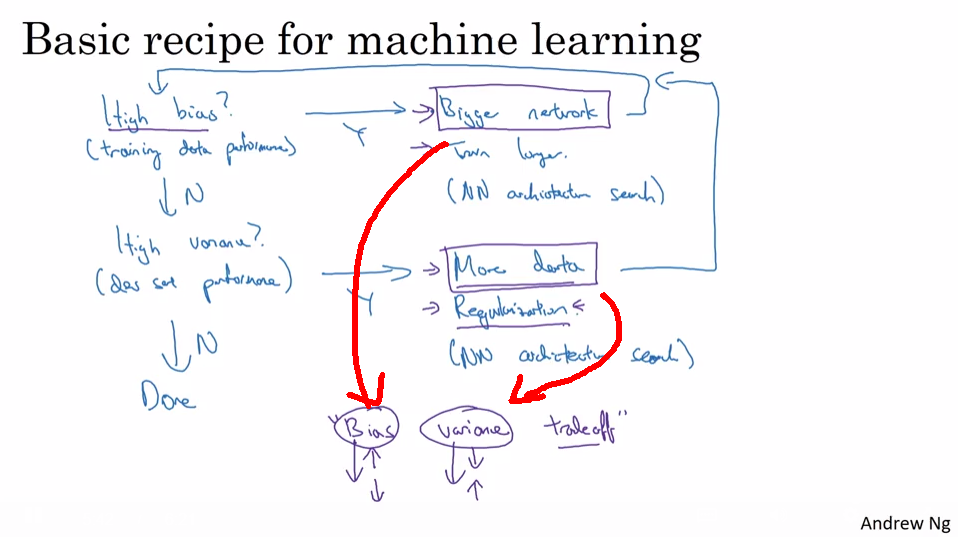
Basic Recipe for Machine Learning
- High bias? (bad train data performance) -> Bigger Network, Train longer, NN Architecture Search
- High variance? (test set performance) -> More data, regularization, NN Architecture Search
Regularization
- $minJ(w, b)$ where $J(w,b) = \frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(\hat{y}^{(i)}, y^{(i)})$
- $w \in \mathbb{R}^{n_x}, b \in \mathbb{R}$
- To add regularization to this function just add $\lambda$ like $ J(w,b) = \frac{1}{m} \sum_{i=1}^{m} \mathcal{L}(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \lvert w \rvert_{2}^{2} + \frac{\lambda}{2m} b^2 $
- $L_2$ regularization = $ \lvert \lvert w \rvert \rvert_{2}^{2} = \sum_{j=1}^{n_x} w_{j}^{2} = w^{T}w $
- $L_1$ regularization = $ \frac{\lambda}{m} \sum_{i=1}^{n_x} \lvert w \rvert = \frac{\lambda}{m} \lvert \lvert w \rvert \rvert_{1}$
- m or 2m in the denominator is just a scaling constant
- $\lambda$ is the regularization parameter and is another hyperparameter in the network
- $J(w^{[1]},b^{[1]}, …, w^{[L]},b^{[L]}) = \frac{1}{m} \sum_{i=1}^{n} \mathcal{L}(\hat{y}^{(i)}, y^{(i)}) + \frac{\lambda}{2m} \sum_{l=1}^{L} \lvert \lvert w^{[l]} \rvert \rvert_{F}^{2} $
- Frobenius Norm = $ \lvert \lvert w^{[l]} \rvert \rvert_{F}^{2} = \sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}} (w_{ij}^{[l]})^{2}$
- $ w : (n^{[l]}n^{[l-1]})$
- $dW^{[l]}$ from backpropagation now becomes $dW^{[l]} + \frac{\lambda}{m}w^{[l]}$
- $L_2$ norm is also sometimes called weight decay
- The regularization multiplies the previous term for a number pretty close to 1, therefore only diminishing its impact
Why regularization reduces overfitting?
- If $\lambda$ is really big the regularization is pushing the weights matrices really close to 0. If many of the weights are 0 is like the neurons are dead so it’s pretty much like you have a much simpler network.
- Thinking with a $tanh$ activation function: if we only focus on variations really close to 0 the variation is roughly linear. If the activation is linear adding layers in a network won’t help them learn non-linear computations.
Dropout regularization
- Probability of “turning off” a given neuron of the layer
- Inverted dropout - ensure that the activations keep the same (the ones that are activated):
- $d3 = np.random.randn(a3.shape[0], a3.shape[1]) < keep_prob$
- $a3 = np.multiply(a3, d3) $
- $a3 = a3 / keep_prob $
- Dropout isn’t used at test time because you don’t want your output to be random
Understanding dropout
- Intuition: Can’t rely on any feature so have to spread out weights
- Cost Function J is no longer well defined so it’s harder to check if it’s going downhill on every iteration. To ensure it’s working correctly with the dropout off the error should monotonically decrease. Another strategy available is to interpolate the error curve into a smooth curve to approximate the original one but still with the dropout on
Other regularization methods
- Data augmentation (image rotation, zooming) -> Easily create more data to train even though the data is not pretty much variated
- Early stopping -> Cheaper to obtain good generalization without having to train for long time. As the weights are initialized close to zero and the weights probably grow over time and keeps fitting the data the early stopping allows the model to have medium weights and good results in shorter amount of time.
- A downsize of early stopping is that is mix two ideas: Optimizing the cost function J (gradient descent, adam) and Not overfitting (regularization). Therefore the early stopping kills this orthogonalization
- L2 regularization is easier to keep each idea separated but several lambda values must be tested and this can be computationally expensive.
Normalizing input
- Normalizing is equals to subtract the mean and then normalize the variance of each feature
- The mean used in the train and test set must be equal as the transformations must be the same
- Why normalize inputs? The minimas might look very elongated and harder to walk through. As the features are normalized the bowl is mostly symmetrical and it’s much easier to walk the gradients errors on it
Vanishing/Exploding Gradients
- Usually happens in very deep neural networks (and long recurrent sequences as well).
- Let’s imagine that yours weights matrices are slightly over 1. The matrices multiplications will produce an exponentially number in respect to the number of layers
- Using the same thinking if the weights are smaller than 1 then the same happens but this time decreasing exponentially
Weight initialization for Deep Networks
- To achieve variance of $var(w) = 2/n$ we can initialize the weights as $np.random.randn(shape) * np.sqrt(2/n^{[l-1]})$
- Xavier activation uses $tanh(\sqrt{\frac{1}{n^{[l-1]}}})$
- Another option is $tanh(\sqrt{\frac{2}{n^{[l]} + n^{[l-1]}}})$
- With this techniques the weights are randomly initialize around zero but either above and below equally reducing the vanishing/exploding gradient problem
Numerical approximation of gradients
- Instead of using just one error to calculate the slope of a given function in a given point it’s better to use two errors (adding one and subtracting one)
- Given $f(\theta) = \theta^3$ and an error $\varepsilon$ the two approximations we’re looking for is $f(\theta + \varepsilon)$ and $f(\theta - \varepsilon)$ because $\frac{f(\theta + \varepsilon) - f(\theta - \varepsilon)}{2 \varepsilon} \approx g(\theta)$
- It runs twice as slow as just checking on one side but it’s much more accurate
- $f’(\theta) = \lim_{\varepsilon \to 0} \frac{f(\theta + \varepsilon) - f(\theta - \varepsilon)}{2 \varepsilon}$ has errors is in the order $O(\varepsilon^{2})$
- $f’(\theta) = \lim_{\varepsilon \to 0} \frac{f(\theta + \varepsilon) - f(\theta)}{\varepsilon}$ has errors is in the order $O(\varepsilon)$ which is squared-ly worse
Gradient Checking
- Concatenate all the flattened weights matrices into a vector $\theta$
- Same with all the derivatives to another vector $d\theta$
- $d\theta_{approx}^{[i]} = \frac{J(\theta_{1}, \theta_{2}, …, \theta_{i} + \varepsilon, …) - J(\theta_{1}, \theta_{2}, …, \theta_{i} - \varepsilon, …)}{2\varepsilon} \approx d\theta[i] = \frac{\partial J}{\partial\theta_{i}}$
- We want to check if $d\theta_{approx}^{[i]} \stackrel{?}{\approx} d\theta$ and for this we can simply compute the normalized euclidean distance of the two vectors as $\frac{\lvert \lvert d\theta_{approx}^{[i]} - d\theta \rvert \rvert_{2}}{\lvert \lvert d\theta_{approx}^{[i]} \rvert \rvert_{2} + \lvert \lvert d\theta \rvert \rvert_{2}}$
- Small values as $10^{-7}$ are great. $10^{-5}$ is okay. $10^{-3}$ is a worrying value indicating large discrepancies
Gradient Checking Implementation Notes
- Don’t use gradient checking in training only in debug
- If algorithm fails grad check, look at the components to try to identify the bug
- Remember that regularization might also be in the loss function and should be considered
- Doesn’t work with dropout because the neurons turned-off will change the behavior on the gradients errors
- Run at random initialization
Quiz
- If you have 10,000,000 examples, how would you split the train/dev/test set?
- 60% train . 20% dev . 20% test
- 98% train . 1% dev . 1% test
- 33% train . 33% dev . 33% test
- The dev and test set should:
- Come from the same distribution
- Come from different distributions
- Be identical to each other (same (x,y) pairs)
- Have the same number of examples
- If your Neural Network model seems to have high bias, what of the following would be promising things to try? (Check all that apply.)
- Make the Neural Network deeper
- Get more test data
- Get more training data
- Add regularization
- Increase the number of units in each hidden layer
- You are working on an automated check-out kiosk for a supermarket, and are building a classifier for apples, bananas and oranges. Suppose your classifier obtains a training set error of 0.5%, and a dev set error of 7%. Which of the following are promising things to try to improve your classifier? (Check all that apply.)
- Increase the regularization parameter lambda
- Decrease the regularization parameter lambda
- Get more training data
- Use a bigger neural network
- What is weight decay?
- The process of gradually decreasing the learning rate during training.
- Gradual corruption of the weights in the neural network if it is trained on noisy data.
- A regularization technique (such as L2 regularization) that results in gradient descent shrinking the weights on every iteration.
- A technique to avoid vanishing gradient by imposing a ceiling on the values of the weights.
- What happens when you increase the regularization hyperparameter lambda?
- Weights are pushed toward becoming smaller (closer to 0)
- Weights are pushed toward becoming bigger (further from 0)
- Doubling lambda should roughly result in doubling the weights
- Gradient descent taking bigger steps with each iteration (proportional to lambda)
- With the inverted dropout technique, at test time:
- You do not apply dropout (do not randomly eliminate units) and do not keep the 1/keep_prob factor in the calculations used in training
- You apply dropout (randomly eliminating units) but keep the 1/keep_prob factor in the calculations used in training.
- You do not apply dropout (do not randomly eliminate units), but keep the 1/keep_prob factor in the calculations used in training.
- You apply dropout (randomly eliminating units) and do not keep the 1/keep_prob factor in the calculations used in training
- Increasing the parameter keep_prob from (say) 0.5 to 0.6 will likely cause the following: (Check the two that apply)
- Increasing the regularization effect
- Reducing the regularization effect
- Causing the neural network to end up with a higher training set error
- Causing the neural network to end up with a lower training set error
- Which of these techniques are useful for reducing variance (reducing overfitting)? (Check all that apply.)
- Dropout
- L2 regularization
- Data augmentation
- Gradient Checking
- Xavier initialization
- Exploding gradient
- Vanishing gradient
- Why do we normalize the inputs xx?
- It makes the parameter initialization faster
- It makes the cost function faster to optimize
- Normalization is another word for regularization–It helps to reduce variance
- It makes it easier to visualize the data